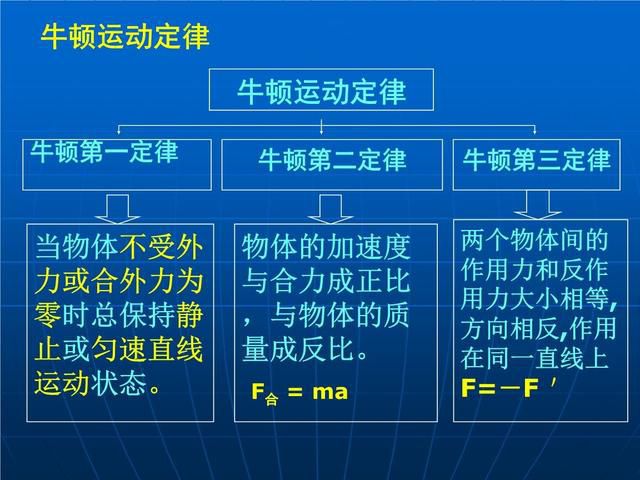
为了验证地面上的引力与地球吸引月球、太阳吸引行星的力是同一种力，遵循同一规律，牛顿进行了著名的“月地”试验。其基本思想是：如果引力与天体间的引力是同一种力，且都与距离的平方成正比，那么月球绕地球做近似圆周运动的向心加速度应该是地面引力加速度的1/3600，因为月球中心到地心的距离是地球半径的60倍。牛顿通过计算证明了自己的想法是正确的。
所谓月地检验，是指牛顿当年思考的一个问题：月球是否也受到地球引力的影响？这种引力和地面上物体受到的引力是否相同（只是大小不同）？
推制工序：
牛顿当时所知道的数据：月球公转周期T（T = 27.3天），月球与地球的距离R = 3.84 * 10^8米，地面附近的重力加速度g = 9.8m/s^2，地球半径R = 6.4 * 10^6米（其实牛顿当时并不知道这个数据，他是根据水手们用的方法算出地球半径的）
1.如果月球绕地球做圆周运动的向心力是由引力提供的，那么它的向心加速度a=GM/R2=g*R^2/R^2=9.8*(6.4*10^6)^2/(3.84*10^8)^2m/s^2=2.72*10^(-3)m/s^2
（GM=g*R^2，即黄金替代公式月球引力常数，M为地球质量，G为引力常数）
2、根据月球绕地球的圆周运动月球引力常数，可得向心力公式为：
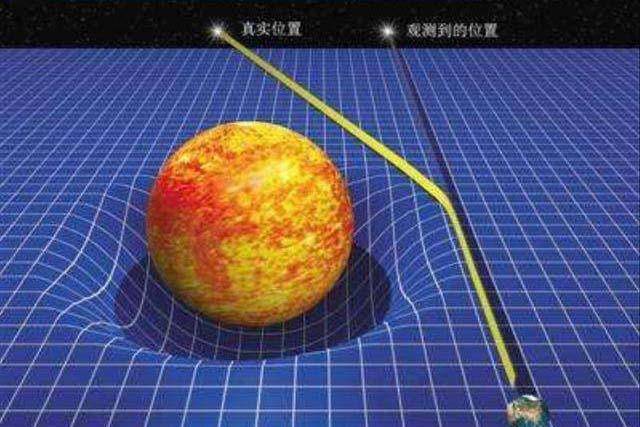
a=2πR/T)^2/R=4π^2R/T^2=4*π^2*3.84*10^8/(27.3*24*3600)^2米/秒^2=2.74*10^(-3)米/秒^2
两种方法得到的向心加速度在误差范围内是相同的。
这样，牛顿的猜想就被检验了。
名师辅导
环球网校
建工网校
会计网校
新东方
医学教育
中小学学历
免费试听
今日
您现在的位置：
