 е…Қиҙ№иҜ•еҗ¬
е…Қиҙ№иҜ•еҗ¬
 жӮЁзҺ°еңЁзҡ„дҪҚзҪ®пјҡ > дәәеҠӣиө„жәҗз®ЎзҗҶеёҲ > дёҖз§ҚеҰӮдҪ•жӣҙеҘҪең°и®°еҪ•ж•°жҚ®valueпјҹ
жӮЁзҺ°еңЁзҡ„дҪҚзҪ®пјҡ > дәәеҠӣиө„жәҗз®ЎзҗҶеёҲ > дёҖз§ҚеҰӮдҪ•жӣҙеҘҪең°и®°еҪ•ж•°жҚ®valueпјҹ жӢҝеҲ°ж•°жҚ®еҗҺпјҢеҫҲеӨҡдәәжҖ»жҳҜд№ жғҜ马дёҠдҪңеӣҫгҖҒи®Ўз®—пјҢ然еҗҺеҫ—еҮәз»“и®ә马дёҠдёҠжҠҘжҲ–еҸ‘еёғгҖӮжҲ‘еңЁжҗңйӣҶиө„ж–ҷж—¶зңӢеҲ°зҡ„еҫҲеӨҡеҢ»еӯҰи®әж–Үз»Ҹеёёиҝҷж ·пјҢеҜ№дёҖз§Қж–°иҚҜжҲ–иҖ…ж–°зҡ„жІ»з–—ж–№жі•иҝӣиЎҢиҜ•йӘҢпјҢе»әдёӘиҜ•йӘҢз»„пјҢеҶҚжүҫдёӘеҜ№з…§з»„пјҢз»ҸиҝҮдёҖж®өж—¶й—ҙжІ»з–—е’Ңи§ӮеҜҹпјҢеҲҶеҲ«ж”¶йӣҶдёҖдёӢжІ»ж„ҲгҖҒжҳҫж•ҲгҖҒжңүж•ҲгҖҒж— ж•Ҳж•°жҚ®пјҢз”ЁеҚЎж–№жЈҖйӘҢдёҖз®—пјҢpеҖје°ҸдәҺ0.05пјҢж•Ҳжһңжҳҫи‘—пјҢеҫҲеҝ«дёҖзҜҮи®әж–ҮжҠҘе‘Ҡз”ҡиҮіи®әж–Үе°ұеҮәжқҘдәҶгҖӮ
дҪҶжҳҜзӯүзӯүпјҢдҪ зңҹзҡ„зЎ®и®ӨдҪ зҡ„еҲҶжһҗжҳҜжҒ°еҪ“зҡ„еҗ—пјҹж•°жҚ®ж”¶йӣҶжҳҜеҗҰйҒөеҫӘдәҶйҡҸжңәжҠҪж ·зҡ„еҺҹеҲҷпјҹжҳҜеҗҰйҮҮз”ЁеҸҢзӣІиҜ•йӘҢпјҹж–№жі•жҳҜдёҚжҳҜеҫ—еҪ“пјҹз»“и®әжҳҜдёҚжҳҜеҗҲзҗҶпјҹжңүжІЎжңүйҒ—жјҸзҡ„з»ҶиҠӮпјҹејӮеёёзҡ„ж•°жҚ®еә”иҜҘеҰӮдҪ•еӨ„зҗҶпјҹиҜ•йӘҢдёӯжңүжІЎжңүе…¶е®ғеӣ зҙ е№Іжү°еҰӮжӣҙжҚўжІ»з–—гҖҒж„ҸеӨ–йҖҖеҮәзӯүзӯүзҡ„еҪұе“ҚпјҹеҰӮжһңдёҚиғҪдҝқиҜҒиҝҷдәӣиҜ•йӘҢжқЎд»¶пјҢеҰӮжһңдёҚиғҪдҝқиҜҒеҜ№ж•°жҚ®еҲҶжһҗи°Ёж…Һзҡ„жҖҒеәҰпјҢиҝҷж ·зҡ„еҲҶжһҗз»“и®әе°ұи°ҲдёҚдёҠеҸҜдҝЎгҖӮ
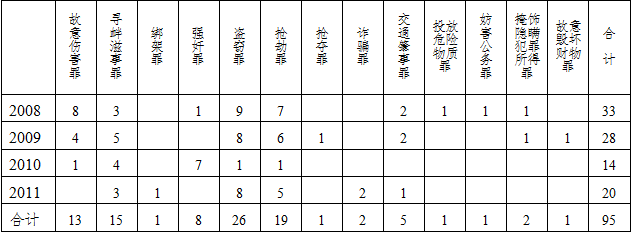
еҸҰеӨ–пјҢеҜ№дәҺејӮеёёж•°жҚ®зҡ„еӨ„зҗҶд№ҹжҳҜз»Ҹеёёзў°еҲ°зҡ„жЈҳжүӢй—®йўҳгҖӮеңЁгҖҠеҘіеЈ«е“ҒиҢ¶гҖӢиҝҷжң¬д№ҰйҮҢе°ұжҸҗеҲ°пјҢеҢ…жӢ¬еӣ дёәзЎ®е®ҡдәҶе…үйҖҹиҖҢиҺ·еҫ—1907 е№ҙиҜәиҙқе°”еҘ–зҡ„иүҫдјҜзү№В·иҝҲе…ӢйҖҠ(Albert Michelson)еңЁеҶ…пјҢеҫҲеӨҡ科еӯҰ家еңЁејҖе§Ӣ他们зҡ„и®Ўз®—еүҚе·Із»Ҹеү”йҷӨдәҶдёҖдәӣж•°жҚ®гҖӮ17 дё–зәӘеҲқе°ұеҸ‘зҺ°иЎҢжҳҹз»•еӨӘйҳід»ҘжӨӯеңҶиҪЁйҒ“иҝҗиЎҢзҡ„科еӯҰ家зәҰзҝ°е°јж–ҜВ·ејҖжҷ®еӢ’(Johannes Kepler)пјҢд»–еңЁз ”究еҸӨеёҢи…ҠеӨ©ж–ҮеӯҰ家зҡ„и®°еҪ•ж—¶пјҢеҸ‘зҺ°жңүдёҖдәӣи§ӮжөӢдҪҚзҪ®и®°еҪ•дёҚз¬ҰеҗҲд»–жӯЈеңЁи®Ўз®—зҡ„жӨӯеңҶиҪЁйҒ“пјҢдәҺжҳҜд»–е°ұеҝҪз•ҘдәҶиҝҷдәӣзјәжҚҹж•°жҚ®(faulty value)гҖӮиҷҪ然зҺ°еңЁдәә们дёҚеҶҚиҪ»жҳ“еү”йҷӨж•°жҚ®пјҢдҪҶиҝҷдәӣејӮеёёж•°жҚ®еҫҖеҫҖдјҡйҖ жҲҗеҲҶжһҗжЁЎеһӢзҡ„еҸҳеҢ–пјҢеҰӮж•°жҚ®дёҚеҶҚжңҚд»ҺжӯЈжҖҒеҲҶеёғпјҢиҝҷе°ұз»ҷеҲҶжһҗеёҰжқҘдәҶеӣ°йҡҫпјҢеӣ жӯӨжңүзҡ„дәәеӣ°йҡҫе°ұдјҡжӮ„жӮ„е°Ҷе…¶еү”йҷӨжҺүжҲ–иҖ…дҝ®ж”№дёҖдёӢж•°еӯ—гҖӮ

еңЁжҲ‘зңӢжқҘпјҢиҝҷдәӣејӮеёёж•°жҚ®еҸҜиғҪи•ҙеҗ«зқҖдё°еҜҢзҡ„дҝЎжҒҜпјҢеә”иҜҘиҖғиҷ‘зҡ„жҳҜйҰ–е…ҲжҺўз©¶ејӮеёёж•°жҚ®дә§з”ҹзҡ„еҺҹеӣ гҖӮеҰӮжһңжҳҜи®°еҪ•й”ҷдәҶдәәе‘ҳдҝЎжҒҜз»ҹи®ЎиҝӣеҚ•дҪҚж—¶й—ҙзҡ„ж„Ҹд№үпјҢеҸҜд»Ҙж”№иҝҮжқҘпјҢ并且жҺўи®ЁдёҖдёӢеҰӮдҪ•жӣҙеҘҪең°и®°еҪ•ж•°жҚ®гҖӮеҰӮжһңжҳҜдёҖдёӘжңүж•Ҳзҡ„ж•°жҚ®пјҢиҰҒд»”з»ҶдәҶи§Јдә§з”ҹиҝҷдёӘж•°жҚ®зҡ„жқЎд»¶пјҢжҳҜеҗҰеңЁиҜ•йӘҢж—¶жқЎд»¶еҸ‘з”ҹдәҶеҸҳеҢ–пјӣеҰӮжһң继з»ӯиҜ•йӘҢпјҢиғҪдёҚиғҪйҮҚзҺ°з»“жһңпјӣжҳҜеҗҰжңүеҝ…иҰҒдҝ®ж”№иҜ•йӘҢи®ЎеҲ’пјҢиҝӣиЎҢиЎҘе……иҜ•йӘҢпјҢд№ҹи®ёж–°зҡ„еҸ‘зҺ°е°ұеӣ иҝҷдёӘејӮеёёж•°жҚ®иҜһз”ҹдәҶгҖӮжҖ»д№ӢеҜ№еҫ…ејӮеёёж•°жҚ®зҡ„еӨ„зҗҶиҰҒйқһеёёж…ҺйҮҚгҖӮ

1975вҖ”1977е№ҙжӢ…д»»иӢұеӣҪзҡҮ家з»ҹи®ЎеӯҰдјҡ第дёҖд»»еҘідјҡй•ҝж–Ҝзү№жӢүВ·еқҺеҲ©еӨ«(Stella Cunliffe)пјҢеңЁ1970 е№ҙиў«и°ғеҲ°иӢұеӣҪеҶ…еҠЎйғЁ(the British Home Office)и°ғжҹҘеұҖпјҢиҝҷдёӘеҚ•дҪҚиҙҹиҙЈиӯҰеҜҹгҖҒжі•йҷўе’Ңзӣ‘зӢұзҡ„зӣ‘зқЈе·ҘдҪңгҖӮ
еңЁеҲ‘дәӢзҠҜзҪӘеӯҰиҝҷдёҖйўҶеҹҹзҡ„дё»иҰҒз ”з©¶е·ҘдҪңпјҢе°ұжҳҜз§ҜзҙҜй•ҝжңҹзҡ„ж•°жҚ®иө„ж–ҷпјҢиҝӣиЎҢеҲҶжһҗпјҢд»ҘеҸ‘зҺ°е…¬е…ұж”ҝзӯ–еҜ№е…¶еҸҜиғҪзҡ„еҪұе“ҚгҖӮеҰӮжңүдёҖйЎ№еҲҶжһҗжҳҜй’ҲеҜ№з”·жҖ§еӣҡзҠҜиҝӣиЎҢзҡ„пјҢеҚіз ”究дёҚеҗҢеҲ‘жңҹзҡ„з”·жҖ§еӣҡзҠҜеҮәзӢұеҗҺдёӨе№ҙеҶ…йҮҚж–°зҠҜзҪӘзҡ„жҰӮзҺҮжңүеӨҡеӨ§гҖӮеҲҶжһҗз»“жһңжё…жҘҡең°иЎЁжҳҺпјҢеҲ‘жңҹи¶ҠзҹӯпјҢйҮҚж–°зҠҜзҪӘзҡ„жҰӮзҺҮи¶Ҡй«ҳгҖӮд»ҺиҖҢдҪңдёәдёҖдёӘиҜҒжҳҺпјҡй•ҝеҲ‘жңҹеҸҜд»ҘжҠҠжғҜзҠҜд»ҺиЎ—еӨҙжё…йҷӨгҖӮеқҺеҲ©еӨ«е№¶дёҚж»Ўи¶ідәҺйҮҚзҠҜзҺҮдёҺеҲ‘жңҹй—ҙз®ҖеҚ•еҜ№жҜ”зҡ„ж•°иЎЁгҖӮеҘ№иҰҒиҝӣдёҖжӯҘеҲҶжһҗж•°иЎЁиғҢеҗҺжүҖйҡҗи—Ҹзҡ„дёңиҘҝгҖӮиҝҷз§ҚжҳҺжҳҫејәе…іиҒ”е…ізі»дё»иҰҒжҳҜеҲ‘жңҹеңЁдёүдёӘжңҲд№ӢеҶ…зҡ„зҠҜдәәйҮҚзҠҜзҺҮй«ҳпјҢз»ҸиҝҮд»”з»ҶжЈҖжҹҘпјҢиҝҷдәӣдәәвҖңеҮ д№ҺйғҪжҳҜдәӣе№ҙиҖҒзҡ„гҖҒеӨ„еўғжӮІжғЁзҡ„гҖҒзІҫзҘһдёҚжӯЈеёёзҡ„дәәпјҢ他们被зІҫзҘһз—…еҢ»йҷўжӢ’д№Ӣй—ЁеӨ–пјҢжүҖд»ҘжүҚдёҖж¬ЎеҸҲдёҖж¬Ўең°еҸҚеӨҚзҠҜзҪӘеҗҺеҶҚиҝӣзӣ‘зӢұгҖӮвҖқиҖҢз»ҹи®ЎиЎЁжүҖеҸҚжҳ зҡ„ж•°еӯ—дәәе‘ҳдҝЎжҒҜз»ҹи®ЎиҝӣеҚ•дҪҚж—¶й—ҙзҡ„ж„Ҹд№үпјҢе®һйҷ…йғҪжҳҜиҝҷеҗҢдёҖжӢЁдәәпјҢиў«еҪ“дҪңдёҚеҗҢдәәйҮҚеӨҚз»ҹи®ЎпјҢжүҚе°ҶзҹӯжңҹзҠҜзҪӘзҡ„йҮҚзҠҜзҺҮеӨёеӨ§дәҶгҖӮз»ҹи®ЎиЎЁдёӯзҡ„еҸҰдёҖдёӘжһҒз«ҜиЎЁзҺ°жҳҜпјҢеҲ‘жңҹеңЁ10 е№ҙд»ҘдёҠзҡ„зҠҜдәәеҮәзӢұеҗҺеҸӘжңү15%зҡ„дәәеҸҲйҮҚж–°зҠҜзҪӘгҖӮеқҺеҲ©еӨ«и®ӨдёәпјҢвҖңиҝҷйҮҢжңүдёҖдёӘеҫҲеӨ§зҡ„е№ҙйҫ„еӣ зҙ пјҢдёҖдёӘеҫҲеӨ§зҡ„зҺҜеўғеӣ зҙ е’ҢдёҖдёӘеҫҲеӨ§зҡ„зҠҜзҪӘзЁӢеәҰеӣ зҙ гҖӮеҲ‘жңҹй•ҝзҡ„йғҪжҳҜдәӣзҠҜеӨ§жЎҲзҡ„дәәпјҢ他们еҮәзӢұеҗҺйҮҚж–°зҠҜеҗҢж ·еӨ§жЎҲзҡ„еҸҜиғҪжҖ§д№ҹдёҚеӨ§дәҶгҖӮвҖқеӣ жӯӨпјҢеңЁеҘ№з”ЁдёӨдёӘжһҒз«Ҝзҡ„жғ…еҶөе°Ҷж•°иЎЁи°ғж•ҙиҝҷеҗҺпјҢйҮҚзҠҜзҺҮе’ҢеҲ‘жңҹй—ҙжҳҺжҳҫзҡ„е…ізі»ж¶ҲеӨұдәҶгҖӮ
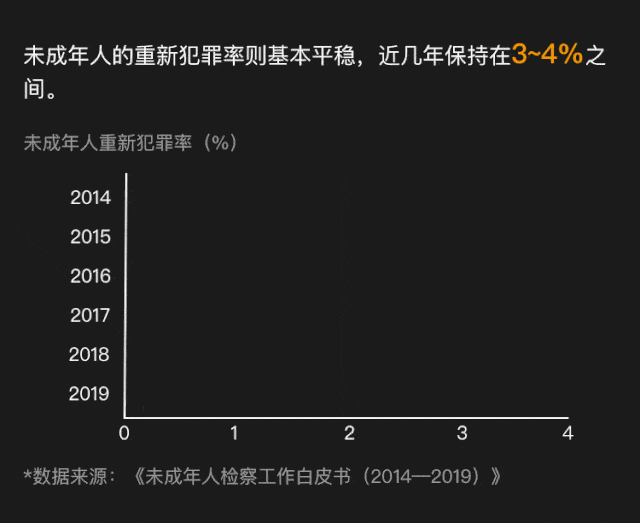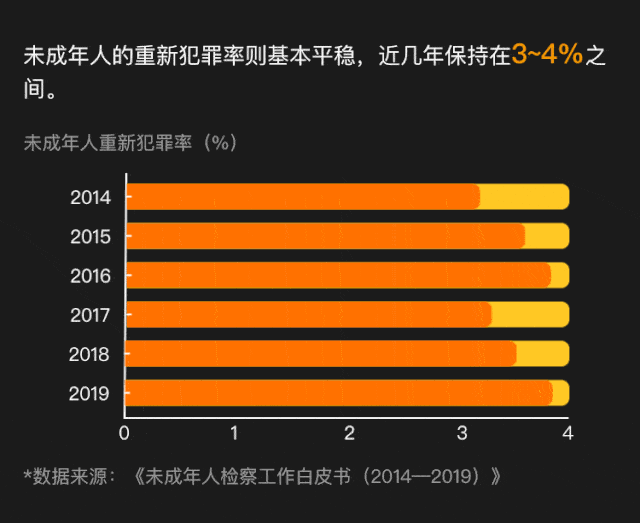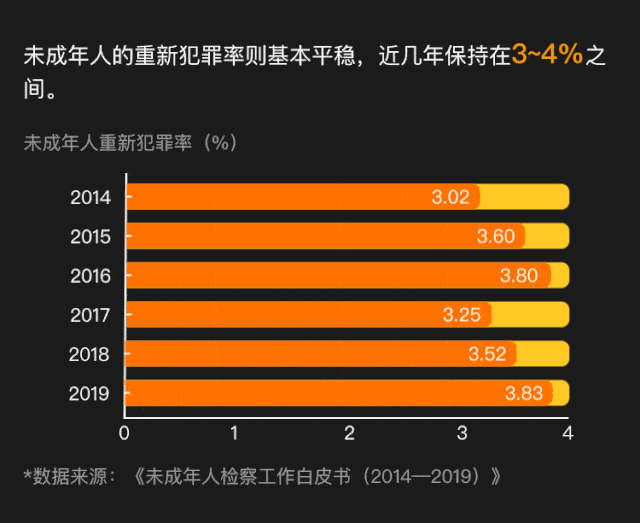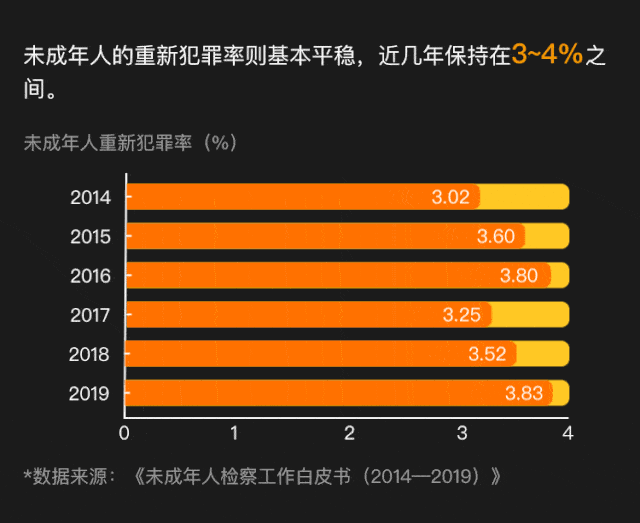
жӣҫд»»иҝҮиӢұеӣҪйҰ–зӣёзҡ„и‘—еҗҚдҪң家иҝӘж–Ҝйӣ·еҲ©иҜҙпјҡжңүдёүз§Қи°ҺиЁҖпјҢи°ҺиЁҖпјҢзіҹзі•йҖҸйЎ¶зҡ„и°ҺиЁҖе’Ңз»ҹи®Ўиө„ж–ҷгҖӮ
жҖ»д№ӢжӢҝеҲ°ж•°жҚ®дёҖе®ҡиҰҒе°ҸеҝғеӨ„зҗҶпјҢжҸҗйҳІеҫ—еҮәй”ҷиҜҜзҡ„з»“и®әгҖӮ
 еҗҚеёҲиҫ…еҜј
зҺҜзҗғзҪ‘ж Ў
е»әе·ҘзҪ‘ж Ў
дјҡи®ЎзҪ‘ж Ў
ж–°дёңж–№
еҢ»еӯҰж•ҷиӮІ
дёӯе°ҸеӯҰеӯҰеҺҶ
еҗҚеёҲиҫ…еҜј
зҺҜзҗғзҪ‘ж Ў
е»әе·ҘзҪ‘ж Ў
дјҡи®ЎзҪ‘ж Ў
ж–°дёңж–№
еҢ»еӯҰж•ҷиӮІ
дёӯе°ҸеӯҰеӯҰеҺҶ